電験１種過去問【2017年機械制御 問4】

解答

公式標準解答

(1) 実軸上の根軌跡の区間は，極0，-1，-2で区切られる区間のうち，右から奇数番目であるから，[-1，0]，[-∞, -2]となる。

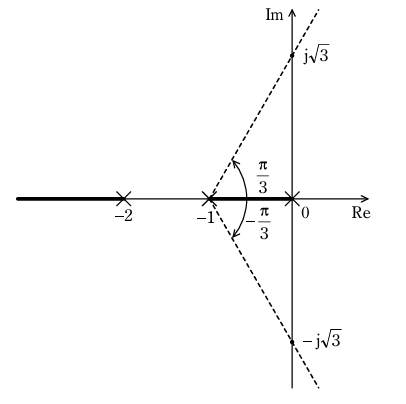
(3) 特性根は0，-1，-2を出発し，K=+∞で三つ全て発散する。漸近線は三本あり，実軸との交点は-1，漸近線の角度は±$\frac{π}{3}$, π である。ただし，角度 π のときは実軸上の軌跡となる。
　まず，0と-1とを出発した二つの特性根は，互いに引き合うように実軸上を移動して0と-1との間で重根となる。その後，分岐して，共役複素根となって±$\frac{π}{3}$の角度の二本の漸近線にそれぞれ近づく。一方，-2を出発した残り一つの特性根は，実根のまま実軸上を左へ移動してK=+∞で-∞となる。すなわち，-2より左側の実軸も根軌跡である。
　これまでに得た結果をまとめると次の図となる。ここで，×印は極，太実線は根軌跡，破線は漸近線をそれぞれ表す。

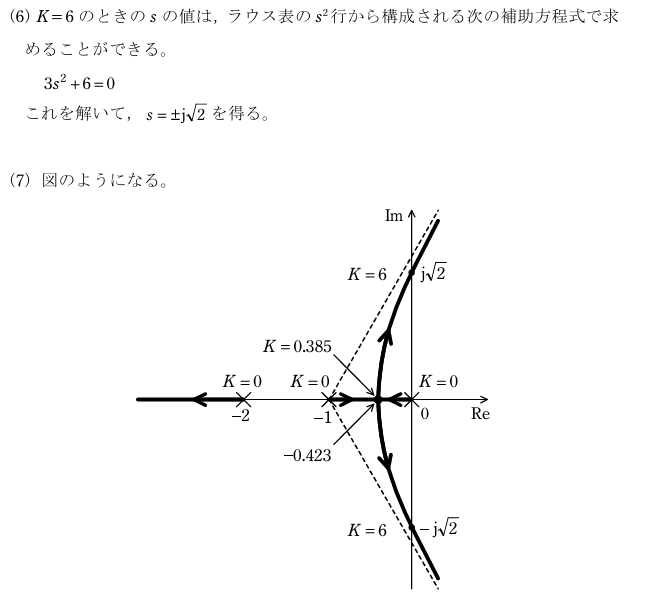
解説

　古典制御からの出題です。一種では現代制御が出題されることが多いです。通常、古典制御はひとひねり加えられる傾向がありますが、本問題は、類題の少なさからかなりの難題といえます。

難易度５（★★★★★）