解答
公式標準解答(※太字は補足)
(1)図1及び同期機の基本式を基にして、無負荷同期機のBC相2線短絡事故時の正相、逆相、零相電圧\(\dot{V}_{1},\dot{V}_{2},\dot{V}_{0}\)及び正相、逆相、零相電流\(\dot{I}_{1},\dot{I}_{2},\dot{I}_{0}\)を発電機の正相誘導起電圧\(\dot{E}\)、零相、正相、逆相インピーダンス\(\dot{Z}_{0},\dot{Z}_{1},\dot{Z}_{2}\)で表せ。
BC相2線短絡事故時の事故点の各相の電圧・電流を
\(\dot{V}_{a},\dot{V}_{b},\dot{V}_{c},\dot{I}_{a},\dot{I}_{b},\dot{I}_{c}\)とすると
\(\dot{V}_{b}=\dot{V}_{c},\dot{I}_{a}=0,\dot{I}_{b}=-\dot{I}_{c}\)となる。
\(\dot{V}_{b}=\dot{V}_{c}\)を対称分で書き表すと
\(\dot{V}_{0}+α^2\dot{V}_{1}+α\dot{V}_{2}=\dot{V}_{0}+α\dot{V}_{1}+α^2\dot{V}_{2}\)となる。
よって、\(\dot{V}_{1}=\dot{V}_{2}\)
また、\(\dot{I}_{a}=0,\dot{I}_{b}=-\dot{I}_{c}\)の関係を対称分で書き表すと
\(\dot{I}_{0}+\dot{I}_{1}+\dot{I}_{2}=0\)
\(\dot{I}_{0}+α^2\dot{I}_{1}+α\dot{I}_{2}=-(\dot{I}_{0}+α\dot{I}_{1}+α^2\dot{I}_{2})\)
よって、\(\dot{I}_{0}=0,\dot{I}_{1}=-\dot{I}_{2}\)
三相交流発電機の基本式に代入すると
\(\dot{E}-\dot{Z}_{1}\dot{I}_{1}=-\dot{Z}_{2}\dot{I}_{2}=\dot{Z}_{2}\dot{I}_{1}\)
\(\dot{V}_{0}=-\dot{Z}_{0}\dot{I}_{0}=0\)
よって、
\(\displaystyle \dot{V}_{1}=\dot{V}_{2}=\frac{\dot{Z}_{2}\dot{E}}{\dot{Z}_{1}+\dot{Z}_{2}},\\
\dot{V}_0=0,\\
\displaystyle \dot{I}_{1}=\frac{\dot{E}}{\dot{Z}_{1}+\dot{Z}_{2}},\\
\displaystyle \dot{I}_{2}=-\frac{\dot{E}}{\dot{Z}_{1}+\dot{Z}_{2}},\\
\dot{I}_0=0
\)
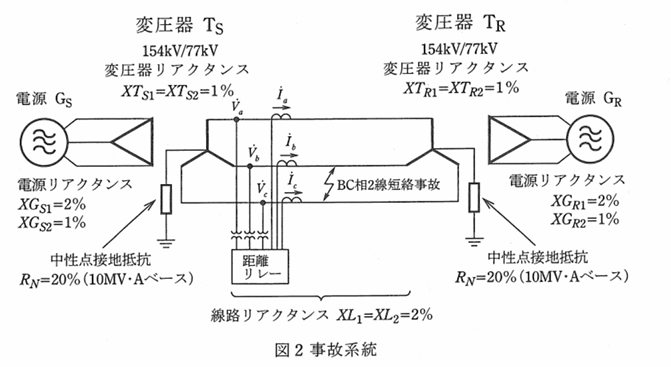
(2)図2に示す系統において、77 [kV] 送電線の中間地点(変圧器 TS 及び TR から等距離の地点)でBC相2線短絡事故が発生した場合、変圧器 TS の 77 [kV] 側出口に設置された距離リレーに入力される各相の電流値及び電圧値(いずれも 77 [kV] 側換算値)を求めよ。ただし、位相については電源 GS の A 相内部誘起電圧を基準とする。また、電源 GS 、GR の内部誘起電圧は 154 [kV] とし、事故点のアーク抵抗及び発電機、変圧器、送電線の抵抗分は無視するものとする。
図中の%インピーダンスの値は、基準容量を 10 [MV・A] ベースとし、基準電圧は各系統電圧で表すものとする。また、添え字1,2は正相及び逆相を表す。
(1)の結果から、BC相2線短絡事故時の対称回路は以下のように表すことができる。
発電機 GS のA相電圧(77kV側換算値)
\(\displaystyle E_{SA}=\frac{77kV}{\sqrt3}\)
とすると、77 [kV] の基準電流は
\(\displaystyle I_{base}=\frac{10 000kV・A}{\sqrt3 ×77kV}\)=74.9806 [A]
また、下図回路は事故点の左右で対称であることから以下の関係が成り立つ。
\(\dot{I}_{S1}=\dot{I}_{R1}=-\dot{I}_{S2}=-\dot{I}_{R2}\)
ここで、\(j7[%]Z_{base}\dot{I}_{S1}=E_{SA}\)であるから、
\(\dot{I}_{S1}=\displaystyle \frac{I_{base}}{j7}×100\)=-j1 071.15 [A]
\(\dot{I}_{S2}=-\dot{I}_{S1}\)=j1 071.15 [A]

この時の各相の電流は以下のようになる。

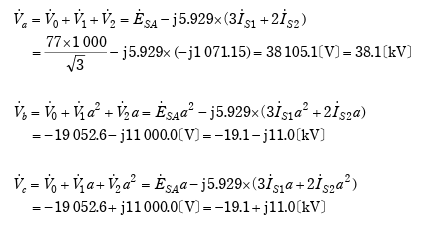
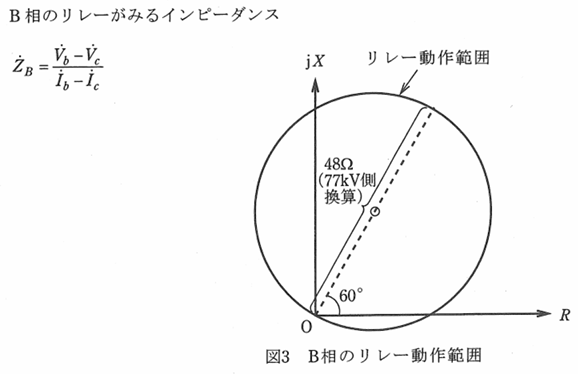
(3)(2)の事故時に B 相の距離リレーがみるインピーダンスを求め、リレーの動作範囲内にあるか判定せよ。ただし、距離リレーがみるインピーダンスは以下の通りとし、B 相のリレーの動作範囲は図3で示される円の内側で設定されているものとする。
題意からB相のみるインピーダンスは次のようになる。
\(\dot{Z}_{B}=\displaystyle\frac{\dot{V}_{b}-\dot{V}_{c}}{\dot{I}_{b}-\dot{I}_{c}}=\frac{-j22 000}{-3710.58}\)=j5.929=j5.93 [Ω]
また、リレー動作範囲は題意から以下の式で与えられる。
\((R-12)^2+(X-12\sqrt3)^2\)<24²
B相リレーのみるインピーダンスを代入すると
\((0-12)^2+(5.929-12\sqrt3)^2\)=364.69<24²=576
となり、動作範囲に入っていることがわかる。
解説
対称座標法を用いての2相短絡故障計算に関する問題です。対象座標法を用いて2相短絡故障の条件付けから関係式の導出の全てを行う必要があり、さらに実務的な回路からの故障時電圧電流から距離リレーの動作判定をすることが求めれられています。このレベルの問題を解答できれば、一種合格も近いです。この問題が難解な場合は、せめて対称座標法の条件式の導出はできるようにがんばってみましょう。
難易度5(★★★★★)



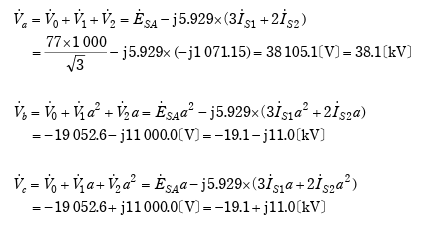

ディスカッション
コメント一覧
まだ、コメントがありません