電験２種過去問【2019年機械 問3】

解答

解説

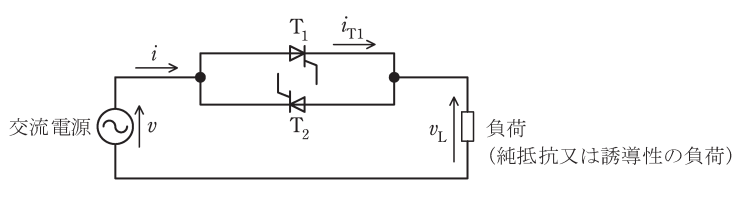
　同じ制御遅れ角で点弧されるサイリスタが逆並列接続された単相交流電力調整装置を図に示す。まず負荷が純抵抗Rの場合の運転について考える。
　電源電圧を$v=\sqrt2V\sin\omega t$とすると、サイリスタ$T_1,T_2$に印加される可能性がある電圧の最大値は$(ﾊ)順方向に\sqrt2V,逆方向に\sqrt2V$である。制御遅れ角$\alpha$で運転したとき、二つあるサイリスタのうち一方のサイリスタ$T_1$に流れる電流$i_{T1}$の平均値$I_{0(av)}$を求めるには、$\omega tが\alphaから\pi$までの負荷電圧波形から1サイクル$(0から2\pi)$の平均値を計算してRで除すればよい。したがって、

$\omega t=\theta$とおくと

$\displaystyle I_{0(av)}=\frac{1}{R}\times\frac{1}{2\pi}\int_{\alpha}^{\pi}\sqrt2V\sin\theta d\theta$

$\displaystyle =\frac{\sqrt2V}{2\pi R}\int_{\alpha}^{\pi}\sin\theta d\theta$

$\displaystyle =\frac{V}{\sqrt2\pi R}[-\cos\theta]_{\alpha}^{\pi}$

$\displaystyle =\frac{V}{\sqrt2\pi R}(-\cos\pi+\cos\alpha)$

$\displaystyle =\frac{V}{\sqrt2\pi R}(1+\cos\alpha)$

$I_{0(av)}=(ｦ)\displaystyle\frac{V}{\sqrt2\pi R}\times(1+\cos\alpha)$となる。使用するサイリスタはこれらの電圧、電流値を参考にして選択される。
　負荷で消費される交流電力は、制御遅れ角$\alpha$によって調整する。$\displaystyle\alphaが\frac{\pi}{2}$のときに負荷で消費される電力は、$\alphaが0$のときに消費される電力に対して$(ｶ)\displaystyle\frac{1}{2}$となる。
　次に、負荷が力率角$\theta$の誘導性負荷の場合の運転について考える。
　この交流電力調整装置で出力の交流電圧すなわち交流電力を調整することができるのは、制御遅れ角$\alpha$を$(ﾄ)\theta<\alpha<\pi$の範囲で運転したときである。負荷が純インダクタンスであったときに、出力の交流電圧を調整できるある制御遅れ角$\alpha_1$で運転したとすると、入力の交流電流は$iは、v$に対して基本波ベースで位相が$\fbox{(ﾇ)90°遅れ}$となり、無効電力の大きさを調整する手段に使われる。