// google adsence用 電験２種過去問【2019年理論 問8】 | 電気主任技術者のいろは

電験２種過去問【2019年理論 問8】

2022年7月10日

【電子回路】演算増幅器の動作《空所問題》

　次の文章は、演算増幅器を用いた回路に関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。ただし、演算増幅器は理想的であるとする。
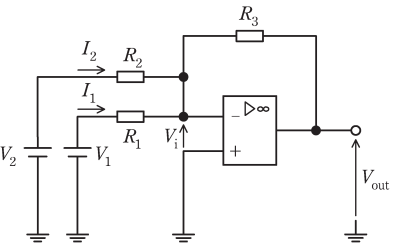
　図の回路において演算増幅器の入力端子間の電圧を\(V_i\)とすると、演算増幅器の電圧増幅度が無限大であるとき\(V_i\)は\(\fbox{（１）}\)となる。これより、抵抗\(R_1\)を流れる電流\(I_1\)は、\(I_1=\fbox{（２）}\)と求められる。演算増幅器の入力端子には電流が流れないことから、抵抗\(R_1\)を流れる電流\(I_1\)と抵抗\(R_2\)を流れる電流\(I_2\)は抵抗\(R_3\)を流れる。その結果、\(R_3\)の両端には大きさが\(\fbox{（３）}\)の電圧が現れる。\(R_1=R_2=R_3=R\)とすると、出力電圧は\(V_{out}=\fbox{（４）}\)となる。この出力電圧より、この回路は\(\fbox{（５）}\)と呼ばれる。

［問８の解答群］

\(\small{\begin{array}{ccc}
(ｲ)&\displaystyle\frac{V_1}{R_1}&(ﾛ)&-(V_1+V_2)&(ﾊ)&1\\
(ﾆ)&R_3(I_1-I_2)&(ﾎ)&R_3I_1I_2&(ﾍ)&\displaystyle\frac{R_1}{V_1}\\
(ﾄ)&R_3(I_1+I_2)&(ﾁ)&積分回路&(ﾘ)&-V_1V_2\\
(ﾇ)&乗算回路&(ﾙ)&\displaystyle\frac{V_1}{R_1+R_3}&(ｦ)&加算回路\\
(ﾜ)&-(V_1-V_2)&(ｶ)&無限大&(ﾖ)&0\\
\end{array}}\)

解答と解説はこちら

解答

\(\small{\begin{array}{cc}
\hline(1)&(ﾖ)&0\\
\hline(2)&(ｲ)&\displaystyle\frac{V_1}{R_1}\\
\hline(3)&(ﾄ)&R_3(I_1+I_2)\\
\hline(4)&(ﾛ)&-(V_1+V_2)\\
\hline(5)&(ｦ)&加算回路\\
\hline\end{array}}\)

解説

　図の回路において演算増幅器の入力端子間の電圧を\(V_i\)とすると、演算増幅器の電圧増幅度が無限大であるとき\(V_i\)は\(\fbox{(ﾖ)0}\)となる。これより、抵抗\(R_1\)を流れる電流\(I_1\)は、\(I_1=(ｲ)\displaystyle\frac{V_1}{R_1}\)と求められる。演算増幅器の入力端子には電流が流れないことから、抵抗\(R_1\)を流れる電流\(I_1\)と抵抗\(R_2\)を流れる電流\(I_2\)は抵抗\(R_3\)を流れる。その結果、\(R_3\)の両端には大きさが\((ﾄ)R_3(I_1+I_2)\)の電圧が現れる。\(R_1=R_2=R_3=R\)とすると、出力電圧は\(V_{out}=(ﾛ)-(V_1+V_2)\)となる。この出力電圧より、この回路は\(\fbox{(ｦ)加算回路}\)と呼ばれる。

<<前問　　次問>>

 

電験２種過去問理論過去問, 電験2種, 理論, 電子回路, 2019年

Posted by ちゅん