電験1種過去問【2020年機械制御 問4】
【自動制御】古典制御におけるベクトル軌跡を用いたフィードバック制御系の解析《計算問題》
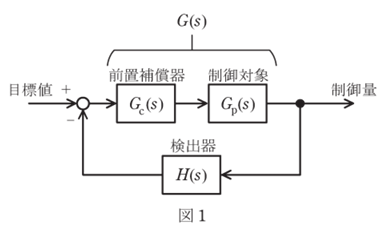
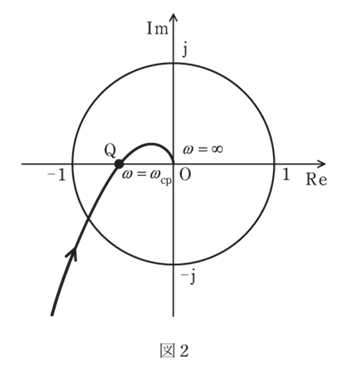
図1に示すフィードバック制御系において、角周波数ω[rad/s]を0から+∞まで変化させたときの一巡周波数伝達関数G(jω)H(jω)のベクトル軌跡が図2であった。ゲイン余裕gmは、線分OQの長さを\(\overline{OQ}\)で表すときgm=20log10\(\frac{1}{\overline{OQ}}\)[dB]で与えられる。位相交差角周波数をωcpとする。次の問に答えよ。
(1)\(\overline{OQ}\)を一巡周波数伝達関数G(jω)H(jω)を用いて表せ。
(2)gm=20[dB]のとき|G(jω)H(jω)|に成立する条件式を対数関数を用いずに示せ。
(3)Gp(s)=\(\frac{1}{(1+3s)(1+7s)}\), Gp(s)=K, H(s)=\(\frac{1}{1+s}\)であるとき、ωcpの値を求めよ。ただし、K>0とする。
(4)小問(3)のとき、ゲイン余裕を20dBとするKの値を求めよ。
(5)小問(3)のとき、制御系を安定限界とするKの値を求めよ。
(6)小問(3)のとき、閉ループ系の特性根λを全て求めよ。
追加学習は自動制御の学習帳で




ディスカッション
コメント一覧
まだ、コメントがありません