解答
(a):（2）が最も近い。
(b):（4）が最も近い。
解説
複素数によるベクトル計算を用いながら、計算をしていく必要があります。電験３種過去問【2019年電力 問16】に全く同じ出題があり、重要な計算手法ですのでしっかり理解しましょう。正答できる方は、是非ベクトル図も書いてみましょう。
(a) 受電端の線間電圧の値 Vr [kV]を求める。
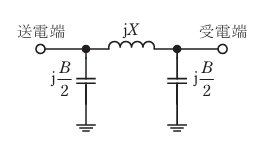
送電端電圧 Vs (相電圧)を基準とすると、送電線路のインピーダンス jX と受電端側のアドミタンス j\(\frac{B}{2}\)に流れる電流 Ir は、
\(\dot{I}_{r}=\frac{\dot{V_{s}}}{jX+\frac{1}{j\frac{B}{2}}}\)
\(=\frac{\frac{66\times10^3}{\sqrt3}}{j200+\frac{1}{j\frac{0.8\times10^{-3}}{2}}}\)
\(=\frac{\frac{66\times10^3}{\sqrt3}}{j200-j2500}\)
\(=j16.567\)[A]
電流 Ir による受電端の電圧 Vr (相電圧)は、
\(\dot{V}_{r}=\dot{I}_r\times\frac{1}{j\frac{B}{2}}\)
\(=j16.567\times (-j2500)\)
\(=41417.5\)[V]
\(=41.4\)[kV]
したがって、受電端の線間電圧は
\(\sqrt3 V_{r}=71.7\)[kV]
(b) 1線当たりの送電端電流の値[A]を求める。
送電端電圧 Vs (相電圧)を基準とすると、送電端側のアドミタンス j\(\frac{B}{2}\)に流れる電流 Is は、
\(\dot{I}_{s}=\frac{\dot{V_{s}}}{\frac{1}{j\frac{B}{2}}}\)
\(=\frac{\frac{66\times10^3}{\sqrt3}}{\frac{1}{j\frac{0.8\times10^{-3}}{2}}}\)
\(=\frac{\frac{66\times10^3}{\sqrt3}}{-j2500}\)
\(=j15.24\)[A]
したがって、送電端電流は
\(\dot{I}_s +\dot{I}_r\)
\(=j31.8\)[A]
