電験３種過去問【2016年電力 問1】

解答

（５）

解説

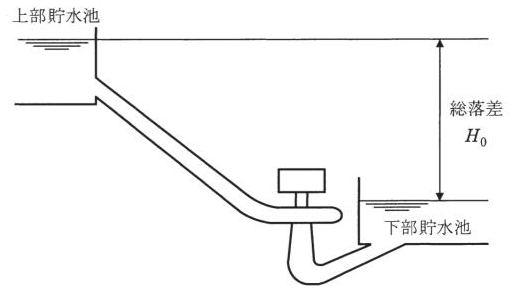
　発電出力は\(\displaystyle P_G=9.8Q_GHη_Gη_T\) [kW]で与えられる。Hは有効落差「総落差－発電損失水頭」であるので、

\(\displaystyle H=H_0(1-h_G)\)となり、

\(\displaystyle P_G=9.8Q_GH_0(1-h_G)η_Gη_T\) [kW]

\(\displaystyle P_G=9.8\times60\times400\times(1-0.03)\times0.87=198485.28≒198500\) [kW]

 

　揚水入力は\(\displaystyle P_P=\frac{9.8Q_PH}{η_Mη_P}\)[kW]で与えられる。Hは「総落差+揚水損失水頭」であるので、

\(\displaystyle H=H_0(1+h_P)\)となり、

\(\displaystyle P_P=\frac{9.8Q_PH_0(1+h_P)}{η_Mη_P}\)[kW]

\(\displaystyle P_P=\frac{9.8\times50\times400\times(1+0.03)}{0.85}=237506≒237500\)[kW]

 

　揚水所要時間T_P[h]は、発電運転時間T_G[h]使用した水量V[m³]と同量を揚水するのにかかる時間である。発電運転時間に使用した水量Vは、

\(\displaystyle V=Q_GT_G\times3600\)[m³]

\(\displaystyle V=60\times8\times3600=1728000\)[m³]

同様にして、揚水ポンプ運転時間に揚水した水量Vは、

\(\displaystyle V=Q_PT_P\times3600\)[m³]が成り立つので、

\(\displaystyle 172800=50\times T_P\times3600\)

\(\displaystyle ∴T_P=\frac{1728000}{50\times3600}=9.6\)[h]

 

　揚水総合効率ηは、同水量での「発電電力量/揚水電力量」である。つまり、

\(\displaystyle 揚水総合効率η=\frac{発電運転時間での発電電力量}{揚水所要時間での使用発電量}\times100\)[%]

\(\displaystyle η=\frac{P_G\times T_G}{P_P\times T_P}\times100\)[%]

\(\displaystyle η=\frac{198500\times 8.0}{237500\times 9.6}\times100=69.6\)[%]