電験２種過去問【2018年電力 問3】
【送電】送電線保護リレー《空所問題》
次の文章は、送電線保護リレーに関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。
\(\fbox{（１）}\)は、平行2回線送電線路の保護リレー方式として、66～77kV級送電線路を主体に広く採用されている。この方式は、保護対象区間の範囲内の１回線事故の場合に、電源端では事故回線に流れる事故電流が健全回線に流れる事故電流と比べて\(\fbox{（２）}\)こと、及び、非電源端では両回線で事故電流の方向が反対になることを利用して事故回線を検出する。
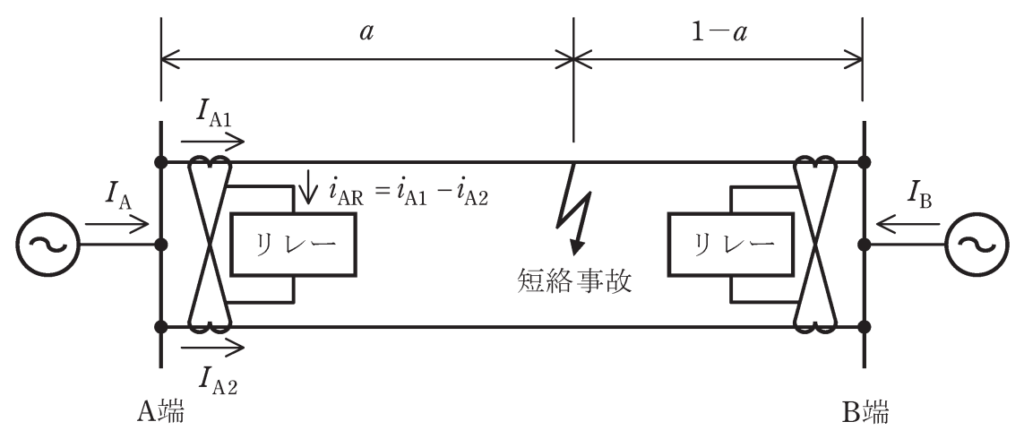
送電線の短絡保護にこの保護リレー方式を適用した、両端が電源端である図の平行２回線送電線路において、A端からの距離の比率がαの地点（A端とB端の間の保護範囲内に限る。）で短絡事故が発生し、A端、B端から短絡電流\(I_{A},I_{B}\)が流入した場合を想定する。また、Ａ端における各送電線の電流\(I_{A1},I_{A2}\)に対する変流器の2次電流を\(i_{A1},i_{A2}\)とすると、Ａ端のリレーに流れる電流\(i_{AR}\)は\(i_{AR}=i_{A1}-i_{A2}\)と表されるものとする。ここで、同じ変流比で\(I_{A},I_{B}\)を変換したものを\(i_{A},i_{B}\)と表すとき、Ａ端のリレーに流れる電流\(i_{AR}\)は\(i_{A},i_{B}\)を用いて\(\fbox{（３）}\)と表される。事故点がＡ端近傍、Ｂ端近傍、及び中間付近の場合で\(i_{AR}\)を比較すると、\(\fbox{（４）}\)の場合に\(i_{AR}\)が最も小さくなり、これがある一定値を下回るとＡ端のリレーは\(\fbox{（５）}\)。
［問３の解答群］
\(\small{\begin{array}{ccc}
(ｲ)&Ｂ端近傍 &(ﾛ)&\displaystyle\left(1-\frac{a}{2}\right)\times i_A+\frac{1-a}{2}\times i_B&(ﾊ)&方向比較リレー方式\\
(ﾆ)&回線選択リレー方式 &(ﾎ)&動作しない &(ﾍ)&大きくなる \\
(ﾄ)&(1-a)\times(i_A+i_B) &(ﾁ)&電流差動リレー方式 &(ﾘ)&誤動作する \\
(ﾇ)&Ａ端近傍 &(ﾙ)&小さくなる &(ｦ)&動作する \\
(ﾜ)&\displaystyle\frac{a}{2}\times i_A-\frac{1-a}{2}\times i_B&(ｶ)&等しくなる &(ﾖ)&中間付近 \\
\end{array}}\)
https://archivelog.net/denken2-kakomon/
https://archivelog.net/denken/