電験2種過去問【2021年理論 問8】
【電気計測】交流ブリッジ回路によるコンデンサの測定《空所問題》
次の文章は、交流ブリッジによるコンデンサの測定に関する記述である。文中の\(\fbox{空白個所}\)に当てはまる最も適切なものを解答群の中から選べ。
図の破線で囲んだ部分は測定対象のコンデンサで、その等価回路は静電容量\(\displaystyle C_1\)と抵抗\(\displaystyle R_1\)の直列回路である。図の\(\displaystyle R_2\)、\(\displaystyle R_3\)及び\(\displaystyle R_4\)は既知の抵抗、\(\displaystyle C_2\)は既知の静電容量、Ⓓは検出器である。また、交流電源の電圧を\(\displaystyle \dot{E}\)、その角周波数をωとする。
今、検出器の指示が零となりブリッジが平衡したとすると、次式が成り立つ。
\(\fbox{(1)}\)
上式から、\(\displaystyle R_1=\)\(\fbox{(2)}\)、\(\displaystyle C_1=\)\(\fbox{(3)}\)が求められる。
電圧\(\displaystyle \dot{E_R}\)、電圧\(\displaystyle \dot{E_C}\)及び電流\(\displaystyle \dot{I}\)をフェザー図で表すと\(\fbox{(4)}\)となる。
フェザー図に記したδの正接である\(\displaystyle tanδ=\)\(\fbox{(5)}\)は誘電正接と呼ばれ、コンデンサの性能を表す指標の一つである。なお、理想的なコンデンサの誘電正接は零となる。

[問8の解答群]
(イ)\(\displaystyle \frac{R_4}{R_2R_3}\) (ロ)\(\displaystyle ωC_2R_3\) (ハ)\(\displaystyle \frac{C_2R_2}{R_4}\)
(ニ)\(\displaystyle \frac{R_3R_4}{R_2}\) (ホ)\(\displaystyle \frac{R_3}{ωC_2}\) (ヘ)\(\displaystyle \frac{C_2R_4}{R_2}\)
(ト)\(\displaystyle \frac{R_2R_3}{R_4}\) (チ)\(\displaystyle \frac{1}{ωC_2R_3}\) (リ)\(\displaystyle \frac{R_2}{C_2R_4}\)
(ヌ)\(\displaystyle \left(R_1+\frac{1}{jωC_1}\right)R_4=\left(R_3+\frac{1}{jωC_2}\right)R_2\)
(ル)\(\displaystyle R_1+R_2+\frac{1}{jωC_1}=R_3+R_4+\frac{1}{jωC_2}\)
(ヲ)\(\displaystyle \left(R_1+\frac{1}{jωC_1}\right)R_2=\left(R_3+\frac{1}{jωC_2}\right)R_4\)
(ワ)
(カ)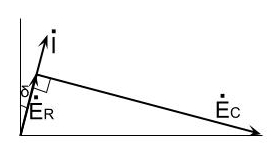
(ヨ)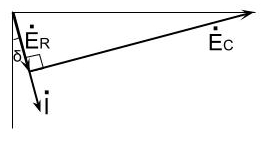
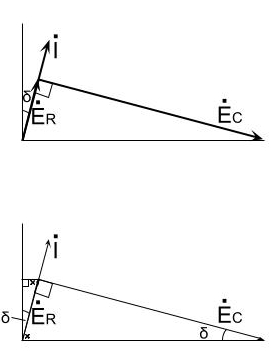


ディスカッション
コメント一覧
まだ、コメントがありません