電験1種過去問【2019年機械制御 問4】
【自動制御】古典制御におけるフィードバック制御系の解析《計算問題》
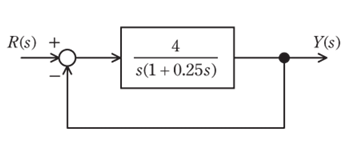
図のようなフィードバック制御系がある。ここで、R(s)とY(s)は、それぞれ目標値r(t)と制御量y(t)のラプラス変換である。次の問に答えよ。
(1)2次遅れ系の標準形 G(s)=\(\frac{ω_n^2}{s^2+2ζω_ns+ω_n^2}\)を考える。ここで、ωn [rad/s] は固有角周波数、ζ は減衰係数であり、ωn > 0、0 < ζ <\(\frac{\sqrt2}{2}\)とする。周波数応答の振幅 |G(jω)| が、|G(jω)|=\(\frac{1}{\sqrt{(1-x)^2+4ζ^2x}}\)で与えられることを示せ。ただし、\(x≜\left(\frac{ω}{ω_n}\right)^2\)とする。
(2)関数 f(x) = (1-x)²+ 4ζ²x を最小にする x を xp とするとき、xp を ζ で表せ。また、周波数応答の振幅 |G(jω)| の最大値 Mp を ζ で表せ。
(3)図のフィードバック制御系の閉ループ伝達関数 Gc(s) を求めよ。また、ωn 及び ζ の値を求めよ。
(4)小問(3)で求めた閉ループ伝達関数 Gc(s) の周波数応答の振幅を最大にする角周波数 ωp [rad/s] 及び最大振幅 Mp の値を求めよ。
追加学習は自動制御の学習帳で




ディスカッション
コメント一覧
まだ、コメントがありません