電験３種過去問【2019年電力 問13】
【送電】電線支線の張力計算《計算問題》
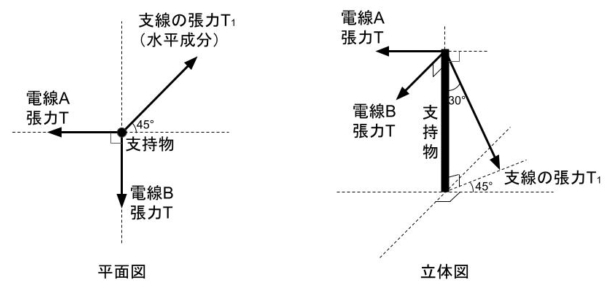
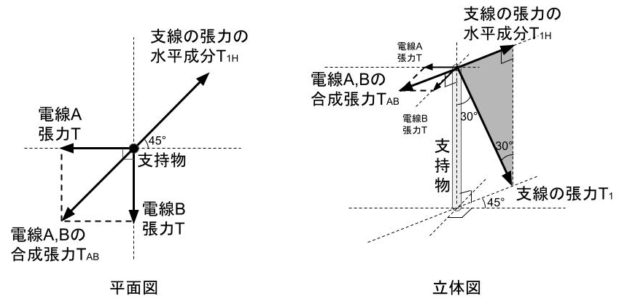
図に示すように、電線A,Bの張力を、支持物を介して支線で受けている。電線A,Bの張力の大きさは等しく、その値をTとする。支線に加わる張力T1は電線張力Tの何倍か。最も近いものを次の（１）～（５）のうちから一つ選べ。
なお、支持物は地面に垂直に立てられており、各電線は支線の取付け高さと同じ高さに取付けられている。また、電線A,Bは地面に水平に張られているものとし、電線A,B及び支線の自重は無視する。
(1)\(\displaystyle \frac{1}{2}\)
(2)\(\displaystyle \frac{\sqrt2}{2}\)
(3)\(\displaystyle \sqrt2\)
(4)\(\displaystyle 2\)
(5)\(\displaystyle 2\sqrt2\)
（５） 上の平面図のように、電線Aの張力Tと電線Bの張力Tは同一平面上にあり、その合成張力TABも同一平面上にある。その大きさは平面図より\(\displaystyle T_{AB}=\sqrt2T\)となる。支線の張力の水平成分T1Hは、電線Aと電線Bの合成張力TABと逆向きで等しい大きさとなる。 一方で、上の立体図のように、支線の張力の水平成分T1Hは、灰色の直角三角形を考えると、\(\displaystyle T_{1H}=T_1 \sin{30°}\)となる。 \(\displaystyle \sqrt2T=T_1 \sin{30°}\) すなわち、支線に加わる張力T1は電線張力Tの\(\displaystyle 2\sqrt2\)倍となる。解答
解説
よって、\(\displaystyle T_{AB}=T_{1H}\)であるので、
\(\displaystyle T_1=2\sqrt2T\)
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/